Začněme tím, co průměr znamená. Průměr řadíme mezi referenční (typické) hodnoty popisné statistiky. Je to určitá vlastnost souboru dat, který zkoumáme. Patří mezi tzv. míry polohy. Máme-li velké množství dat, tak pomocí nějaké míry polohy můžeme data popsat – patří sem různý typy průměrů, medián, modus, střední hodnota. V tomto článku se zaměříme na průměry v Excelu.

Průměry v Excelu, matematice a statistice

Existuje 6 základních typů průměrů, které popisují data.

• Aritmetický průměr
• Vážený průměr
• Klouzavý průměr
• Geometrický průměr
• Harmonický průměr
• Kvadratický průměr

Harmonický a Kvadratický průměry jsou poměrně specifické a příliš se s nimi v praxi nesetkáme – přidávám odkaz na Wikipedii. Ostatní typy popíšu níže s tím, že vysvětlím jak daný průměr funguje a jak se počítají průměry v Excelu i s příkladem.

Aritmetický průměr – PRŮMĚR (AVERAGE)

Aritmetický průměr je nejjednodušším typem a patří mezi nejvíce používaní průměry v excelu. Vyskytuje se nejčastěji v uvažování a také v různých výpočtech běžné populace. Tento průměr má ale své výrazné nedostatky. Asi každý někdy z nás slyšel o nějaké statistice typu průměrné mzdy.

Průměrná mzda ale velmi špatně popisuje výběrový soubor – tj mzdy běžné populace, protože reálně ve mzdách existují značné nerovnosti.

V Excelu se Průměr počítá pomocí funkce =PRŮMĚR (v anglické variantě excelu AVERAGE). Na příkladu níže máme 5 zaměstnanců z nichž poslední 2 mají zcela nadstandardní příjmy.

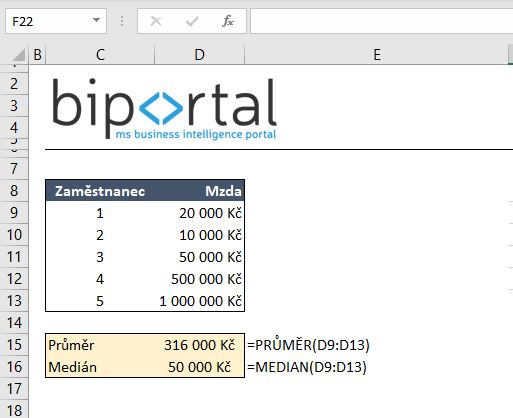
Vidíme, že průměr v tomto případě zcela chybně popisuje výběrová data a je vhodnější data popsat pomocí mediánu. Pokud by ale rozdíly ve mzdách mezi zaměstnanci nebyly vysoké, tak průměr a medián by byla podobná čísla.

Vážený průměr – Excel Funkce SOUČIN.SKALÁRNÍ()/SUMA() nebo =SUMPRODUCT()/SUM()

Vážený průměr je již daleko užitečnější popisná charakteristika. Pokud máme nějaká data, která mají různou důležitost, tak pomocí tohoto průměru dokážeme tuto důležitost jednotlivých hodnot v průměru zohlednit. Matematický vzorec najdeme třeba na Wikipedii. K použití váženého průměru v Excelu lze použít techniku článku v odkazu.

Typickým příkladem použití je například pokud máme skupinu několika úvěrů, které mají různou úrokovou sazbu. Dejme tomu, že bychom chtěli spočítat průměrnou úrokovou sazbu.

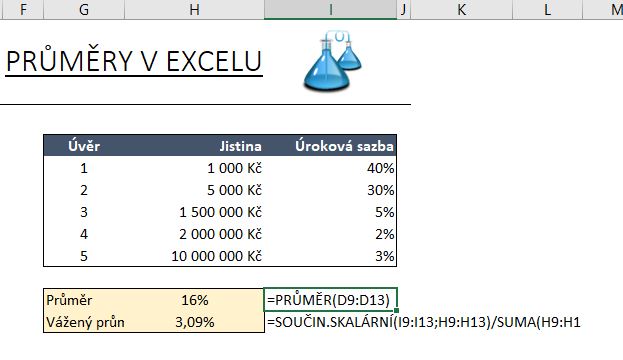
Obyčejným průměrem dostaneme hodnotu pro úrokovou sazbu 16%. To je ale špatně, protože úvěry s nejvyššími sazbami mají minimální jistinu. Pokud chceme, aby byla ve výsledku zohledněna váha jistiny úvěru, tak musíme použím vážený průměr.

Geometrický průměr – Excel Funkce GEOMEAN()

Geometrický průměr je charakteristika, která se nejvíce používá pro vypočítání průměru pokud máme statistický soubor např s tempy růstu v čase (třeba růsty HDP). Počítáme jej podobně jako aritmetický průměr, jen se místo sčítání (aritmetický průměr) používá násobení a místo dělení (aritmetický průměr) se používá odmocnina.

Tento průměr jsem celkem podrobně rozebral v článku – Geometrický průměr v Excelu (GEOMEAN) – Jak na to?

Klouzavý průměr – Excel Funkce PRŮMĚR(<hodnoty za určitý počet období>)

Klouzavý průměr je průměrem za určitý daný počet hodnot. Existuje více typů z nichž základním je jednoduchý klouzavý průměr, který tu ukážu. Vedle toho ještě existuje např. exponenciální klouzavý průměr.

Tyto průměry se často používají k vyhlazení nějakého volatilního souboru dat. Reálné využítí si můžeme ukázat na vývoji kurzu EUR/CZK za rok 2019. Klouzavý průměr je mnoho za sebou jdoucích obyčejných průměrů dopočítaných pomocí funkce =PRŮMĚR.

V případě 7-mi deního klouzavého průměru vezmeme vždy pro každý řádek do průměru posledních 7 hodnot (viz obrázek).

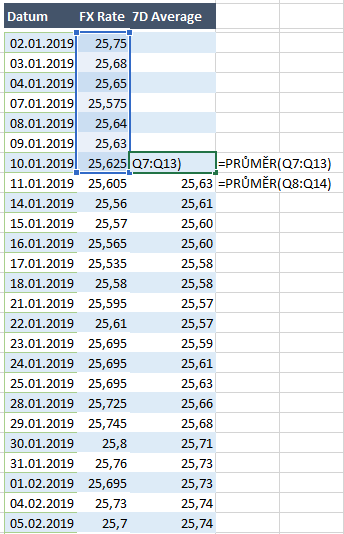
Pokud si obě časové řady zobrazíme v grafu, tak vidíme, že 7D klouzavý průměr data vyhlazuje. Čím delší období klouzavého průměru, tím bude křivka pložší a více vyhlazená.

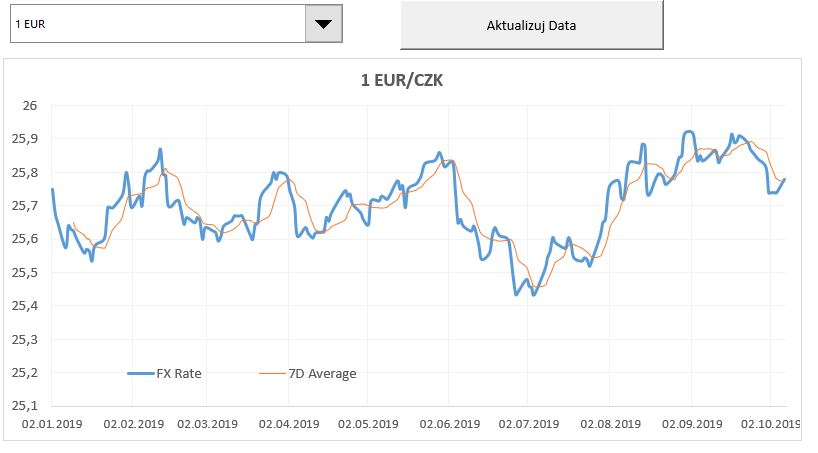
Časté využití je při analýze cenných papírů nebo FX měn a derivátů. Příznivci tzv technické analýzy věří, že pokud kurz akcie nebo nějakého jiného finančního instrumentu protnou dlouhodobý klouzavý průměr (zespoda nebo shora), tak je to signál k nákupu/prodeji.