Lately, I’ve been dedicating a lot of time to financial mathematics in Excel. I’ll try to leverage that and shift the focus from Excel to SQL Server. Perhaps someone is considering creating an application for amortization calculator schedule where you can input parameters, and it will generate results for you in a table.

The result of my efforts will be an SQL procedure called [Get_Amortization_schedule], which takes parameters like @Loan_Value, @Loan_Term_Years, @Interest_rate, and @Payment_frequency. This procedure returns a table, which represents the amortization schedule. I will use this schedule for reporting through SQL Server Reporting Services.

By the way, this procedure can come in handy even if you don’t want to report the amortization schedule through Reporting Services but want to load data into Excel using an SQL procedure (you can check how to do it here).

How an Amortization Schedule Looks and Its Components (Preparation Before Programming)

The goal is to create an SQL script that will accept certain parameters and, when executed, generate an amortization schedule as you typically see in various calculators.

Note: An amortization schedule contains a list of regular payments sent to the bank at certain intervals. Typically, payments are made monthly (but it’s not always a requirement).

What an Amortization Schedule Typically Contains

• Date or payment sequence number (for a 30-year loan, the schedule will contain 30 * 12 = 360 records).
• Loan balance at the beginning of the period.
• Annuity payment – calculated using a formula.
• Interest – calculated as [Loan balance at the beginning of the period] * [Loan interest rate].
• Principal – calculated as [Annuity payment] – [Interest].
• Loan balance at the end of the period.

Info: The loan balance at the end of the period for the last payment is always 0, indicating that the loan has been fully repaid.

Steps for Constructing the Schedule Sequentially

1. Prepare a table with as many records as the number of payments (depends on the loan length and payment frequency).
2. Calculate the annuity payment – you can calculate the regular payment using a formula (see the link above).
3. Initial loan balance = loan balance at the end of the previous payment.
4. Calculate interest.
5. Calculate principal.
6. Loan balance at the end of the period = [Initial loan balance] – [Principal].

SQL Procedure for Generating an Amortization Schedule and Annuity Payment

The procedure accepts 4 parameters:

• @Loan_Value – loan amount.
• @Loan_Term_Years – loan term in years.
• @Interest_rate – annual interest rate.
• @Payment_frequency – payment frequency (the procedure supports 2 options: monthly and yearly).

What the procedure does:

• At the beginning, it declares variables @Loan_term_formula and @Interest_rate_formula and calculates the number of payments and interest rate based on the @Payment_frequency parameter.
• Calculates the annuity into the @Annuity variable.
• Creates temporary tables and inserts the first payment.
• Loops to calculate the remaining rows into the temporary table.

CREATE PROCEDURE Get_Amortization_schedule (
  @Loan_Value DECIMAL (15,2)
  ,@Loan_Term_Years INT
  ,@Interest_rate FLOAT
  ,@Payment_frequency VARCHAR(255)
)
AS
DECLARE @Loan_term_formula INT = CASE WHEN @Payment_frequency = 'Monthly' THEN @Loan_Term_Years*12 ELSE @Loan_Term_Years END
DECLARE @Interest_rate_formula FLOAT = (CASE WHEN @Payment_frequency = 'Monthly' THEN @Interest_rate/12 ELSE @Interest_rate END)/100
DECLARE @Annuity FLOAT

SET @Annuity = @Loan_Value * (POWER(1+@Interest_rate_formula,@Loan_term_formula) * ((1 + @Interest_rate_formula)-1))
/
(POWER(1+@Interest_rate_formula,@Loan_term_formula)-1)

DROP TABLE IF EXISTS #Schedule

SELECT
  CAST(1 AS INT) AS [Payment_Number]
  ,CAST(@Loan_Value AS MONEY) AS [Balance_Start]
  ,CAST(@Annuity AS MONEY) AS [Annuity payment]
  ,CAST(@Loan_Value * @Interest_rate_formula AS MONEY) AS [Thereof: Interest]
  ,CAST(@Annuity - (@Loan_Value * @Interest_rate_formula) AS MONEY) AS [Ammortization]
  ,CAST(@Loan_Value - (@Annuity - (@Loan_Value * @Interest_rate_formula)) AS MONEY) AS [Balance_End]
INTO #Schedule

DECLARE @Loop_Payment_Nr as INT = 1
WHILE @Loop_Payment_Nr <= @Loan_term_formula
BEGIN 
INSERT INTO #Schedule (
  [Payment_Number]
  ,[Balance_Start]
  ,[Annuity payment]
  ,[Thereof: Interest]
  ,[Ammortization]
  ,[Balance_End]
)
SELECT 
  [Payment_Number] = @Loop_Payment_Nr
  ,[Balance_Start] = [Prev_row].[Balance_End]
  ,[Annuity payment] = @Annuity
  ,[Thereof: Interest] = @Interest_rate_formula * [Prev_row].[Balance_End]
  ,[Ammortization] = [Prev_row].[Annuity payment] - (@Interest_rate_formula * [Prev_row].[Balance_End])
  ,[Balance_End] = [Prev_row].[Balance_End] - ([Prev_row].[Annuity payment] - (@Interest_rate_formula * [Prev_row]. [Balance_End]))
FROM
(SELECT
  [Payment_Number]
  ,[Balance_Start]
  ,[Annuity payment]
  ,[Thereof: Interest]
  ,[Ammortization]
  ,[Balance_End]
FROM #Schedule
WHERE Payment_Number = @Loop_Payment_Nr - 1
) AS [Prev_row]
SET @Loop_Payment_Nr = @Loop_Payment_Nr +1
END 

SELECT

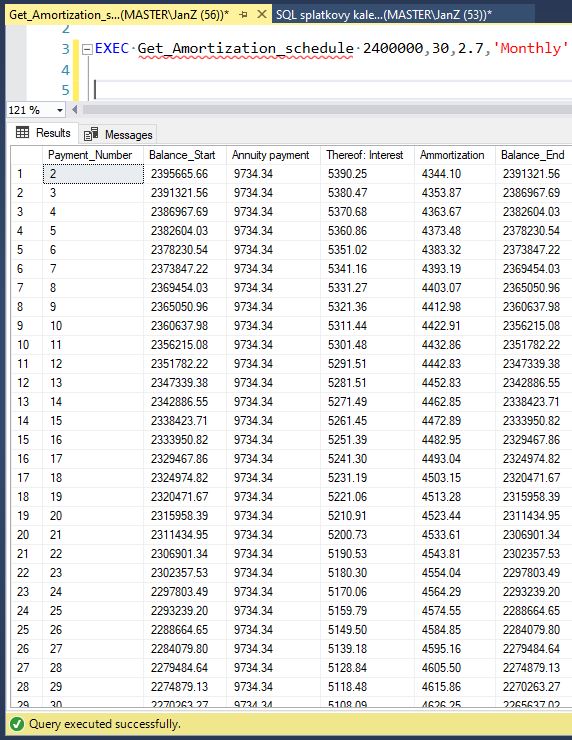
I’ll create and test the procedure. You can compare the results with an online installment calculator; they should match.

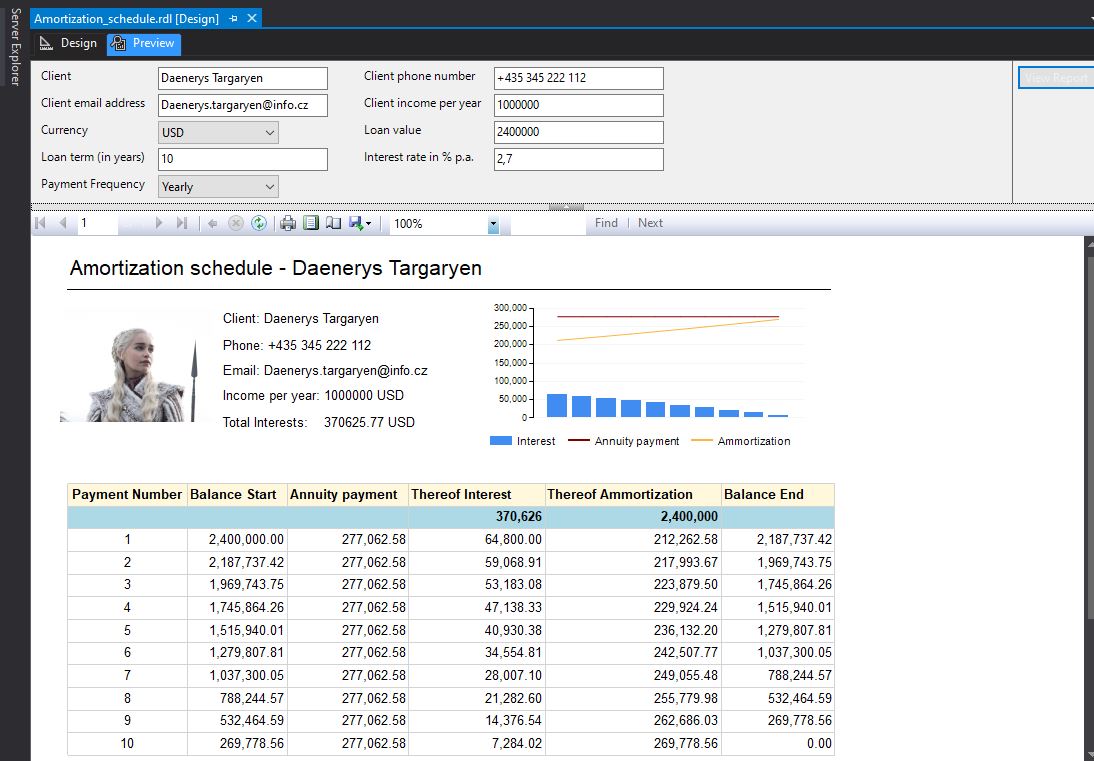
SSRS Report as an Installment Calculator for Daenerys Targaryen

If I have an SQL procedure (or any other object), I can call it from an application. I will send the result to Reporting Services and configure some parameters like Client and Loan parameters. Loan parameters will be sent to the procedure, which will return the result, and client parameters will be displayed in a printable report.

For a $2,400,000 USD loan, a term of 30 years, an interest rate of 2.7%, and monthly payment frequency, it will generate 360 payments with an annuity payment of $9,734 USD.

If we change the term to 10 years and the payment frequency to yearly, logically, only 10 payments should be generated, and at the end of the 10th year, the loan should be fully paid off. In this case, the annuity payment is $277,062 USD.